| Wave of Sound の研究月誌 |
|
第1部 いくつかのシンプルな考察 2 持続可能となるための条件 前節では2つの簡単な例で、財政収支が黒字でも累積債務が発散してしまう場合もあれば、財政収支が赤字でも累積債務が持続可能な場合もあることを説明した。そして、債務が持続可能である条件は、債務にかかる平均金利より経済の成長率が大きいことである、と述べた。この節では、この事実を数式(数列の漸化式)を用いて証明しよう。 簡単のため、経済の成長率を一定であると仮定し、文字 a で表す(注1)。例えば成長率が5%ならば a= 0.05 である。その意味は、名目の国民総所得(文字 Y で表す)の毎年の増加率が a であるということだ。最初の年の国民総所得をY0 、翌年のそれをY1 、翌々年のそれをY2 、一般に n 年目のそれをYn と下に添え字をつけて表せば、Y1 = (1+a)Y0 、 Y2 = (1+a)Y1 などの関係がある。これらはまとめて Yn+1 = (1+a)Yn ( n=0,1,2, ... ) (式1) という漸化式で表すことができる。 経済成長にともなって、政府支出や税収も同じ成長率で増加すると仮定しよう。言いかえると、政府支出や税収が国民総所得に占める比率が変わらない、と仮定する。その結果、財政赤字が国民総所得に占める比率も変わらない。その比率をd とする。例えば、毎年、政府が国民総所得の6%の赤字を出し続けている国の場合には、d=0.06 である。よって、n 年目の財政赤字をDnで表せば Dn = d Yn と書くことができる。 n 年目の(期首の)債務残高Bn がいくらになるかを求めよう。一般に、翌年の債務残高Bn+1 は、当年の債務残高Bn に、利息と財政赤字Dn を加えたものであるから(注:赤字は期末決算時に生じるものと見なしている) 翌年の債務残高=今年の債務残高+平均金利×今年の債務残高+財政赤字 これを式で表せば、 Bn+1 = Bn + r Bn + d Yn (式2) となる。ここで r は債務にかかる平均金利で一定と仮定している。これらの式から、毎年の債務残高を順に計算していくことができる。 しかし、興味があるのは債務残高そのものより、むしろその国民総所得に対する比率 B/Y である。そこで、式2の両辺を、式1で割り算すると(つまり、左辺どうし右辺どうし割り算すると)、求めたい比率が満たす次の漸化式を得る。 ( 1 + a ) Bn+1/Yn+1 = ( 1 + r ) Bn/Yn + d この2項間漸化式は容易に解けて、n 年目の比率をn の式で表すことができる。結果は
となる( n=0,1,2, ... ) 。右辺は2つの項を足したものからなる。第1項は定数、第2項は等比数列である。 ■結果からわかること 公比 (1 + r )/(1 + a ) が 1 より大きい場合には、n →∞の未来において債務の比率 Bn/Yn が発散してしまう。つまり、平均金利が名目成長率よりも大きい ( r > a )場合には、累積債務は持続可能ではない。 逆に、公比が1よりも小さい場合には、債務の比率は一定の値 d /(a-r ) に限りなく近づく。つまり、 名目成長率が平均金利を上回っているならば、累積債務の比率が発散することはない。 後者の場合に債務の比率が限りなく近づいていく値は、他の条件によらず 赤字比率/(名目成長率 −平均金利) に等しい。とくに、この極限値は初年度や途中での債務残高の比率には無関係である。例えば、財政赤字が国民総所得の4%、名目成長率が5%、債務にかかる平均金利が2%で一定ならば、現在の債務残高がどれだけであろうと遠い将来には、累積債務は国民総所得の1.333...倍に近づく。 以上の考察からわかることは2つある。 第1に、累積債務が持続可能であるためには、名目成長率をなるべく高くしつつ、同時に、平均金利をそれより低く保つ必要がある。 第2に、上の条件が満たされていても、外的ショックに対する安全率を確保するために、名目成長率と平均金利の差はできるだけ大きいことが望ましく、かつ、その差にくらべて赤字比率が大きすぎないことが望ましい。 赤字比率は小さいほうが望ましいけれども、マイナスにする(つまり財政収支を黒字化する)ことが絶対に必要なわけではない、ということも強調しておきたい。払わなければならない犠牲(社会福祉水準の低下や失業、少子化など)が大きすぎるならば、名目成長率が平均金利を上回っている状況下で、あえて歳出削減や増税をおこなって財政収支を黒字化したり、赤字比率を極端に小さく保つ必然性はないのである。 第2節の注 注1) この節の議論では成長率などを一定と仮定しているが、この仮定は弱めることができる。たとえば、名目成長率や平均金利が一定ではなくても、前者が後者を常に上回っていて、かつ、その差の最小値が正ならば、累積債務が持続可能となることが証明できる。 (2007年1月作成 2007年1月29日 更新) |
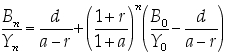 (式3
(式3