財政赤字の持続可能性について

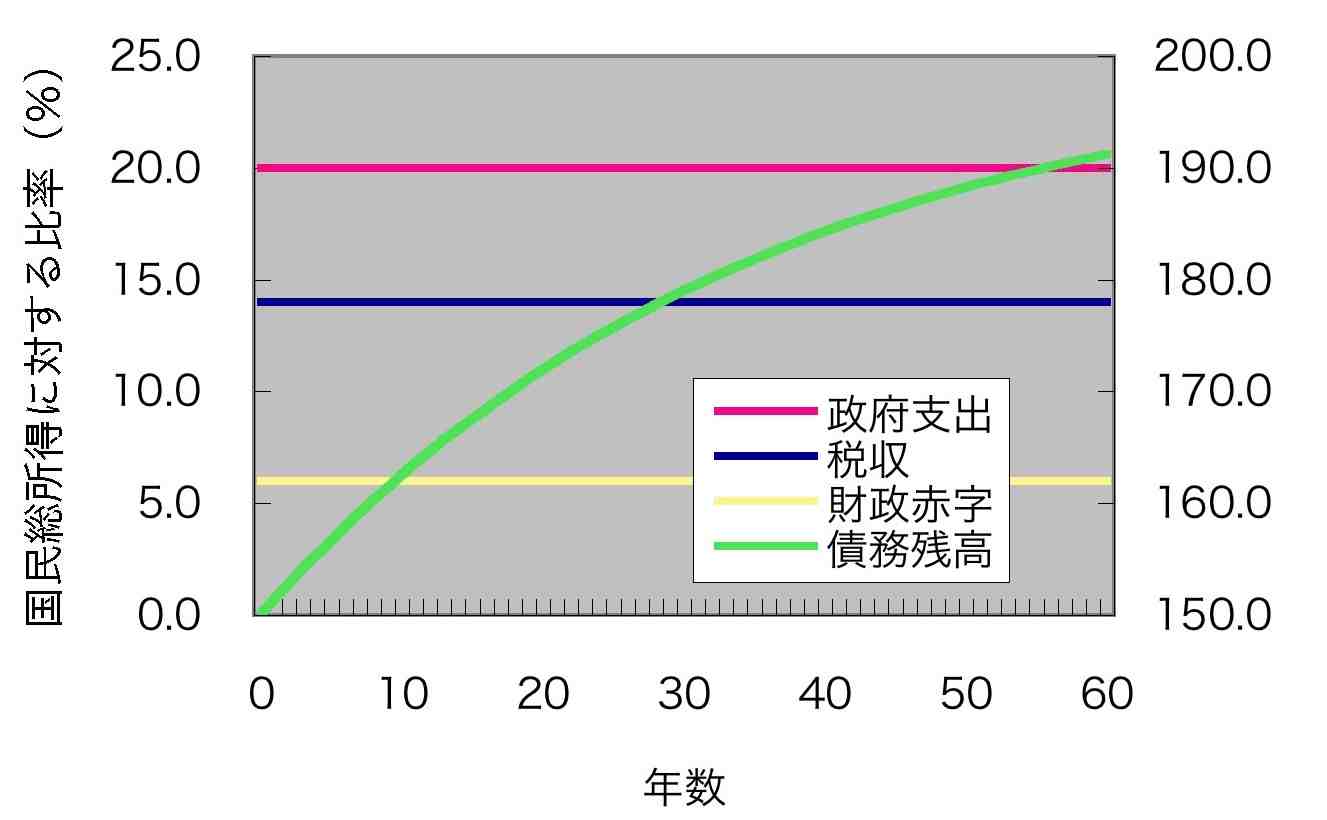
第１部　いくつかのシンプルな考察

１　プライマリーバランスは重要でない

政府の債務残高の比率を小さくするために、利払いや利息の受取を除いた収支（プライマリーバランス＝基礎的財政収支）の黒字回復は絶対に必要なのだろうか。

調べてみるとそうではないことがわかる。財政収支が黒字でも債務残高が発散してしまうケースがある一方で、財政収支が赤字でも債務残高が維持可能となるケースもある。財政収支の黒字化は必要条件ではない。より重要なのは、経済の成長率を長期金利より高く維持することである。

■ケース1

それを簡単な具体例で見てみよう。少しばかりの算数とのおつきあいをお許し願いたい。経済規模（ＧＮＩ＝国民総所得）が 500兆円のとある国で、（利払いを除いた）政府支出がちょうどその２割の100兆円だが、税収が70兆円しかないとしよう。財政赤字は30兆円である。 この赤字分の資金を政府は国債発行などにより調達しなければならない。

しかしそれだけでは足りない。これまでの累積債務が（金融資産を差し引いた正味で）計750兆円あり、利払 いも必要である。それにかかる利息を平均で2％とすれば、利息は15兆円になる。つまり、今年、新たに発行する必要のある国債は30兆円ではなく45兆円である。これまで の750兆円に、この45兆円を加えた計795兆円の債務が翌年へと引き継がれる。

では、翌年はどうだろうか。国の経済規模は年とともに大きくなる（もちろん、例外的なときもあるが、一般的な経験としてはそうである）。それとともに、政府支出や税収、財政赤字も変わる。では、どのように変わるだろうか。

それらは、短期的な変動を除いて考えるなら、経済規模（国民総所得）と同じ割合で増える、と仮定するのが自然で ある（詳しくは末尾の注1を参照）。なぜなら、国民や政治家が、政府の規模や税率の大幅な変更を望むのでない限り、国の経済に占める公的サービスの割合や、 そのための税負担の割合が、大きく変わるとは考えにくいからだ。

そこで仮に、名目の成長率が5％であると仮定してみよう。来年の経済規模は今年より5％増えて1.05倍に なる。すると政府支出や税収なども1.05倍になるだろう。計算すると、国民総所得は525兆円、政府支出は105兆円、税収は73.5兆円。それで、来年の 利払いを除いた赤字は31.5兆円に増える（ちょうど5％の増加である）。

累積債務の方はどうなるだろうか。平均利率が2％で変わらないとすれば、795兆円にかかる利息は15.9 兆円。これに上で計算した財政赤字31.5兆円を加えて、47.4兆円の資金が不足するから、この分を国債発行などでまかなう必要がある。それを、これま での795兆円に加えて、計842.4兆円の債務がさらに翌年へと引き継がれる。

このようにして債務残高はねずみ算式にどんどん増えていくが、その金額そのものは重要ではない。たとえば5 万円は子供にとっては大金だが、大人にとっては必ずしもそうではないであろう。金額そのものよりも、財布の大きさに対する比率が重要である。同様に国の場 合にも、債務残高そのものよりも、経済規模（国民総所得）に対する割合を考える必要がある。

計算を続けていった場合の、債務残高の国民総所得に対する割合（％）の推移を示したのが次の図1である。名目成 長率は5％、平均利率は2％で一定、政府支出と税収が国民総所得に占める割合も一定で、したがって財政赤字が国民総所得に占める割合も6％で一定であると仮定し た。（これをケース１と呼ぶ。）

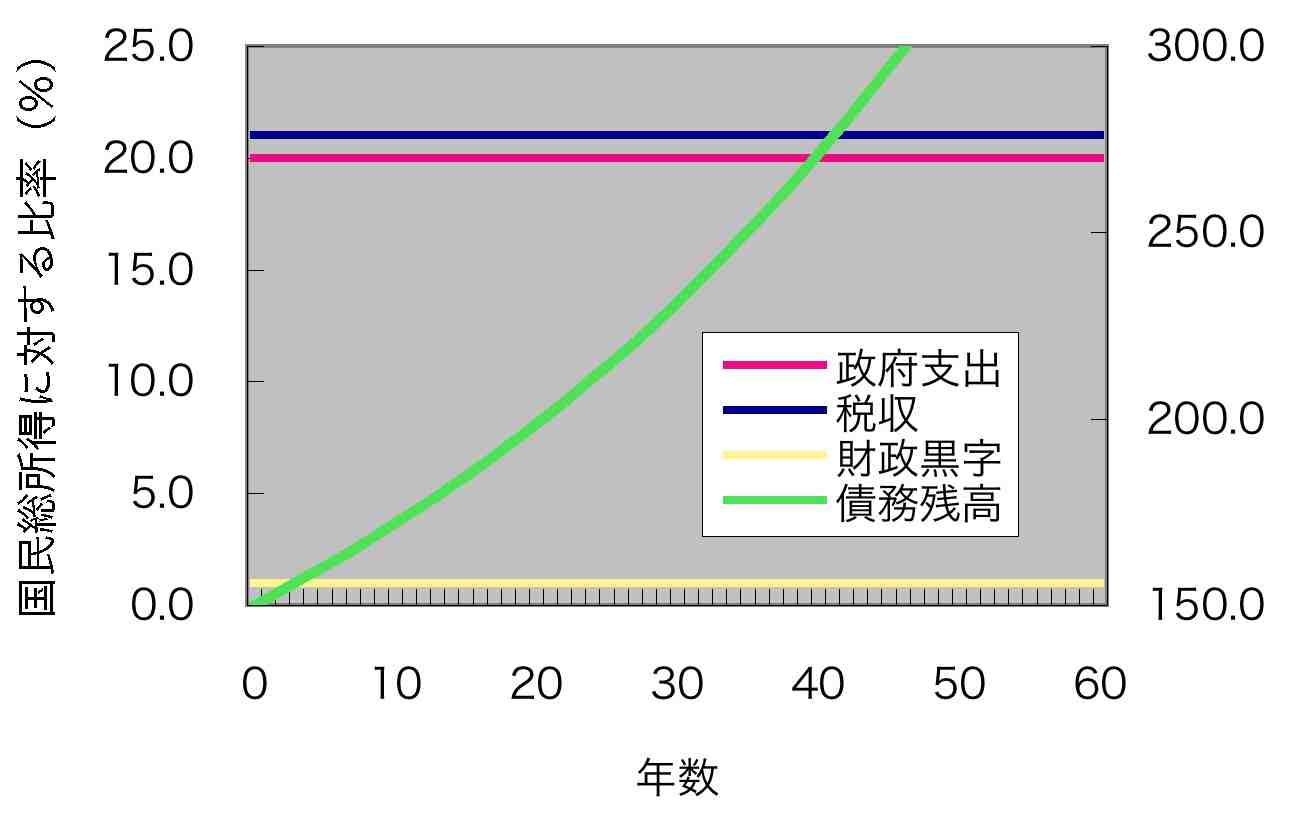
図1　債務残高などの推移 （ケース1）　（債務残高のみ右目盛）

債務残高の割合は、はじめ増えるがやがて増加がゆるやかになり、一定の割合に近づいていくことがわかる（次 節で示すように、この場合には債務残高の割合は2、つまり200％に限りなく近づいていく）。債務残高の割合が発散してしまって破産するようなことはな い。すなわち、（金利や成長率が一定とした仮定のもとで）累積債務は持続可能である。

財政赤字の額そのものは毎年5％ずつ増えているにもかかわらず、なぜ持続可能となるのかといえば、それは経 済規模がどんどん大きくなるので、はじめの債務残高やそれに対する利払い負担（今の場合は利率2％）が年を経るにつれ、相対的に小さく感じられるようにな るからである。

■ケース2

別の場合を考えてみよう。今度は、政府が歳出削減あるいは増税をして、財政は黒字になり、その黒字を債務の 返済に充てるとしよう。黒字が国民総所得に占める割合が1％で一定であったとする。その代わり成長率は低下する。名目成長率は0％、平均利率は2％で一定であ ると仮定して、さきほどと同様の計算をしてみよう（ケース2と呼ぶ）。次の図2は経済規模が500兆円、政府支出が100兆円、税収が105兆円、黒字が 5兆円の場合を示している。

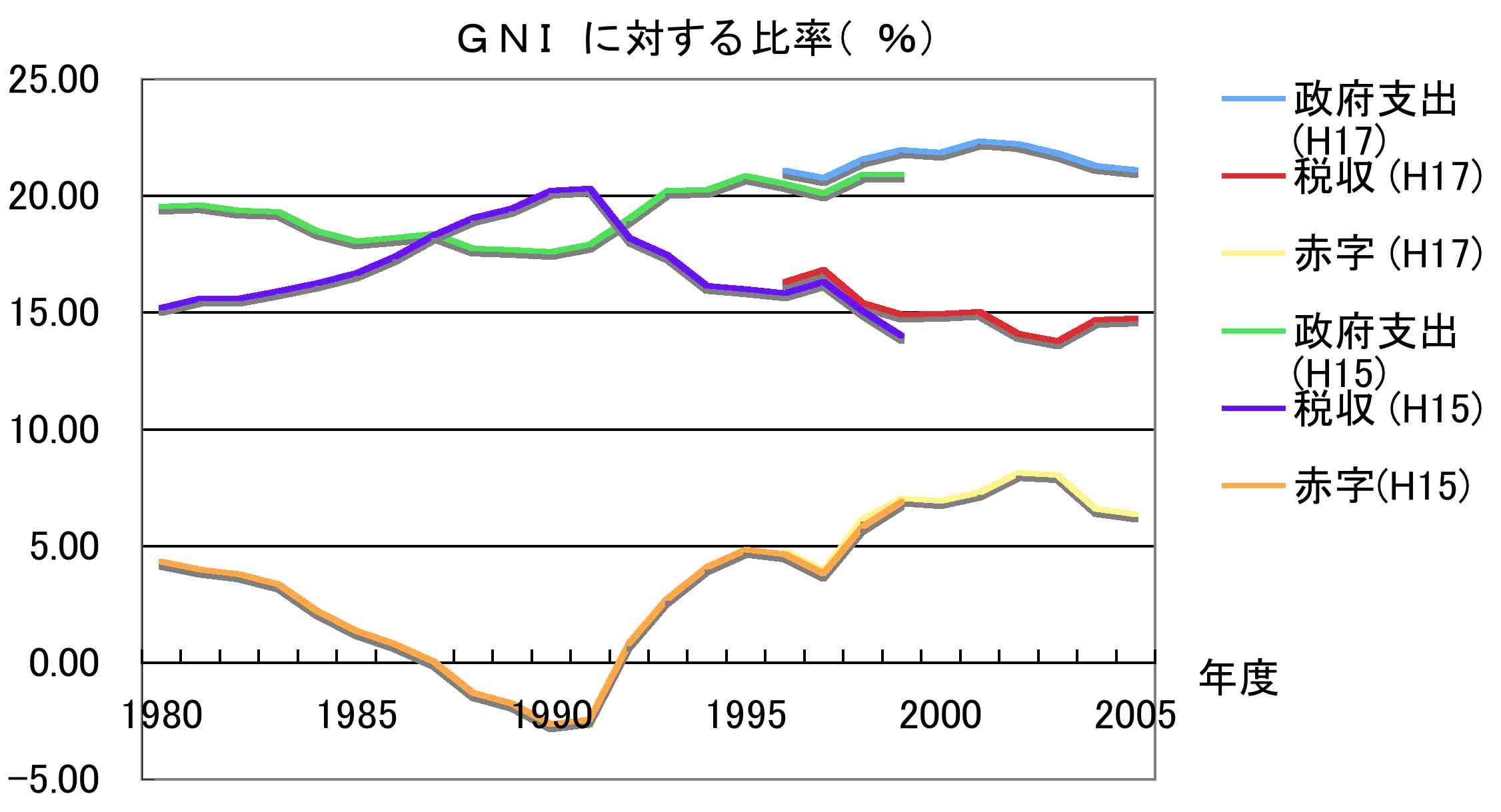
図2　債務残高などの推移（ケース2）　（債務残高のみ右目盛）

図2からわかるように、累積債務の対国民総所得比率は増え続け、発散してしまう。これは持続可能ではない。現実 にはどこかの段階で、誰も国債を買わなくなり、国債の価格が暴落（利率は急上昇）して、破産することになるだろう。財政収支が黒字であるにもかかわらず、 持続可能でなくなるのは、経済が成長しない状況下で財政黒字を上回る利払い負担があるために、債務残高が増え続けるからである。

■累積債務が持続可能である条件

ケース１のように、基礎的財政収支が赤字でも累積債務が持続可能な場合もあれば、ケース２のように、黒字で も持続可能でない場合もある。その違いはどこにあるか、といえば、経済の名目成長率と、債務にかかる平均利率のどちらが大きいかである。次節で示すよう に、名目成長率が平均利率を上回っていれば累積債務は長期的には持続可能であり、そうでなければ持続不可能である。

ちょっと驚かれるかもしれないが、この持続可能かどうかを決める条件に、財政赤字が国民総所得に占める割合や現 在の債務残高は無関係である。財政赤字の割合がどれほど大きくても、また、債務残高が現在どれほど膨れあがっていても、名目成長率が平均利率を上回ってい れば持続可能だし、そうでなければ持続不可能である。

もちろん、名目成長率が平均利率を上回っていても、あまりに大きな財政赤字や債務残高があれば、市場が不安 になって国債を買わなくなり利率が上がるので、上の話が成り立たなくなる、ということはあるかも知れない。経済に短期的なショックが加わる場合には、その ような心理は増幅される。だから、安全率を確保するために、財政赤字や累積債務の対国民総所得比率の水準にはそれなりの限度というものがあるだろう。こうした 心理的・現実的な制約があることを承知の上で理屈を述べるなら、名目成長率が平均利率を上回っていれば債務残高の比率が発散することはない、ということは 真理である。

次節では、いま述べたことを数式（数列の漸化式）を用いて証明する。証明は必要なときに見ればよい、という方は、高度成長期以降の日本で名目成長率と平均利率の関係がどう推移してきたか、を概観する次次節へと進んでいただければ、と思う。

第1節の注

注1）次に示す図3は、近年の日本における政府支出（利息や配当の支払いや受け取りを含む）と税収の、ＧＮＩ （国民総所得）に対する比率の推移である。財政収支はバブル期の数年を除いて、赤字が続いていることがわかる。97年度のこぶは、消費税導入に伴う前年度 の駆け込み需要の好況とその後の景気冷え込みによる。

図３　政府支出や税収の割合はおおむね一定

政府支出の比率はおおむね20％程度である。ここ15年ほどの増加傾向は社会保障費の増加による。最近数年の微減は、地方政府の公共事業など、社会保障費以外の支出の削減による。

税収の比率も、バブル期に20％近くまで増えるなど景気による変動はあるが、おおむね15％程度とみなせる。

景気変動の影響は比率にして5％くらいである。税収の方が政府支出より景気変動 の影響をより強く受ける。政府支出の増減がゆるやかなためである。好況時には税収の比率が大きく増え、政府支出の比率は少し減少する。逆に不況時には税収 の比率が大きく減り、政府支出の比率が少し増加することが読みとれる。だから財政収支の黒字化には好況の方が有利である。当然のことではあるが。

（上のグラフの1999年度以前の数値は国民経済計算（９３ＳＮＡ）の平成15年度確報を、1996年度以 降の数値は平成17年度確報をもとに計算している。接続領域で多少の不突合が見られるが、傾向を把握するのに支障はない。なお、ここでいう政府とは、国民 経済計算における一般政府のことであり、地方政府や社会保障基金などを含む。政府支出のうち社会保障については、社会保障負担（保険料など）を控除した純 給付のみをカウントしている。同様に、税収には社会保障負担を加え、社会保障給付を控除している。国鉄長期債務、国有林野庁債務の政府への承継（一般政府 から居住者への資本移転：1998年度約27兆円）などの特殊要因は除いてある。特殊要因について詳しくは「内閣府経済社会総合研究所　ESRI Discussion Paper No.167 国民経済計算から見た日本経済の新動向」（Web上で入手可）の第3章注5を参照。政府支出や税収の内訳の推移についての詳細な分析も参考になる。注5に 付け加えると、厚生年金基金の代行部分の積立金の、厚生保険特別会計への返上（居住者から社会保障基金への資本移転）は2005年度3.5兆円である。）

ホーム　目次　次へ進む

(2007年1月作成　 2007年1月30日 更新)